Universal property

In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.

This article gives a general treatment of universal properties. To understand the concept, it is useful to study several examples first, of which there are many: all free objects, direct product and direct sum, free group, free lattice, Grothendieck group, product topology, Stone–Čech compactification, tensor product, inverse limit and direct limit, kernel and cokernel, pullback, pushout and equalizer.

Contents

Motivation

Before giving a formal definition of universal properties, we offer some motivation for studying such constructions.

Formal definition

Suppose that U: D → C is a functor from a category D to a category C, and let X be an object of C. Consider the following dual (opposite) notions:

An initial morphism from X to U is an initial object in the category (X \downarrow U) of morphisms from X to U. In other words, it consists of a pair (A, φ) where A is an object of D and φ: X → U(A) is a morphism in C, such that the following initial property is satisfied:

A terminal morphism from U to X is a terminal object in the comma category 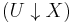(U \downarrow X) of morphisms from U to X. In other words, it consists of a pair (A, φ) where A is an object of D and φ: U(A) → X is a morphism in C, such that the following terminal property is satisfied:

The term universal morphism refers either to an initial morphism or a terminal morphism, and the term universal property refers either to an initial property or a terminal property. In each definition, the existence of the morphism g intuitively expresses the fact that (A, φ) is "general enough", while the uniqueness of the morphism ensures that (A, φ) is "not too general".

Duality

Since the notions of initial and terminal are dual, it is often enough to discuss only one of them, and simply reverse arrows in C for the dual discussion. Alternatively, the word universal is often used in place of both words.

Note: some authors may call only one of these constructions a universal morphism and the other one a co-universal morphism. Which is which depends on the author, although in order to be consistent with the naming of limits and colimits the latter construction should be named universal and the former couniversal. This article uses the unambiguous terminology of initial and terminal objects.

Examples

Below are a few worked examples, to highlight the general idea. The reader can construct numerous other examples by consulting the articles mentioned in the introduction.

Tensor algebras

Let C be the category of vector spaces K-Vect over a field K and let D be the category of algebras K-Alg over K (assumed to be unital and associative). Let

U : K-Alg → K-Vect

be the forgetful functor which assigns to each algebra its underlying vector space.

Given any vector space V over K we can construct the tensor algebra T(V) of V. The tensor algebra is characterized by the fact:

“Any linear map from V to an algebra A can be uniquely extended to an algebra homomorphism from T(V) to A.”

This statement is an initial property of the tensor algebra since it expresses the fact that the pair (T(V), i), where i : V → T(V) is the inclusion map, is an initial morphism from the vector space V to the functor U.

Since this construction works for any vector space V, we conclude that T is a functor from K-Vect to K-Alg. This means that T is left adjoint to the forgetful functor U (see the section below on relation to adjoint functors).

Products

A categorical product can be characterized by a terminal property. For concreteness, one may consider the Cartesian product in Set, the direct product in Grp, or the product topology in Top.

Let X and Y be objects of a category D. The product of X and Y is an object X × Y together with two morphisms

π1 : X × Y → X
π2 : X × Y → Y

such that for any other object Z of D and morphisms f : Z → X and g : Z → Y there exists a unique morphism h : Z → X × Y such that f = π1∘h and g = π2∘h.

To understand this characterization as a terminal property we take the category C to be the product category D × D and define the diagonal functor

Δ : D → D × D

by Δ(X) = (X, X) and Δ(f : X → Y) = (f, f). Then (X × Y, (π1, π2)) is a terminal morphism from Δ to the object (X, Y) of D × D. This is just a restatement of the above since the pair (f, g) represents an (arbitrary) morphism from Δ(Z) to (X, Y).

Limits and colimits

Categorical products are a particular kind of limit in category theory. One can generalize the above example to arbitrary limits and colimits.

Let J and C be categories with J a small index category and let CJ be the corresponding functor category. The diagonal functor

Δ : C → CJ

is the functor that maps each object N in C to the constant functor Δ(N): J → C to N (i.e. Δ(N)(X) = N for each X in J).

Given a functor F : J → C (thought of as an object in CJ), the limit of F, if it exists, is nothing but a terminal morphism from Δ to F. Dually, the colimit of F is an initial morphism from F to Δ.

Properties

Existence and uniqueness

Defining a quantity does not guarantee its existence. Given a functor U and an object X as above, there may or may not exist an initial morphism from X to U. If, however, an initial morphism (A, φ) does exist then it is essentially unique. Specifically, it is unique up to a unique isomorphism: if (A′, φ′) is another such pair, then there exists a unique isomorphism k: A → A′ such that φ′ = U(k)φ. This is easily seen by substituting (A′, φ′) for (Y, f) in the definition of the initial property.

It is the pair (A, φ) which is essentially unique in this fashion. The object A itself is only unique up to isomorphism. Indeed, if (A, φ) is an initial morphism and k: A → A′ is any isomorphism then the pair (A′, φ′), where φ′ = U(k)φ, is also an initial morphism.

Equivalent formulations

The definition of a universal morphism can be rephrased in a variety of ways. Let U be a functor from D to C, and let X be an object of C. Then the following statements are equivalent:

The dual statements are also equivalent:

Relation to adjoint functors

Suppose (A1, φ1) is an initial morphism from X1 to U and (A2, φ2) is an initial morphism from X2 to U. By the initial property, given any morphism h: X1 → X2 there exists a unique morphism g: A1 → A2 such that the following diagram commutes:

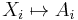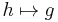If every object Xi of C admits a initial morphism to U, then the assignment X_i \mapsto A_i and h \mapsto g defines a functor V from C to D. The maps φi then define a natural transformation from 1C (the identity functor on C) to UV. The functors (V, U) are then a pair of adjoint functors, with V left-adjoint to U and U right-adjoint to V.

Similar statements apply to the dual situation of terminal morphisms from U. If such morphisms exist for every X in C one obtains a functor V: C → D which is right-adjoint to U (so U is left-adjoint to V).

Indeed, all pairs of adjoint functors arise from universal constructions in this manner. Let F and G be a pair of adjoint functors with unit η and co-unit ε (see the article on adjoint functors for the definitions). Then we have a universal morphism for each object in C and D:

Universal constructions are more general than adjoint functor pairs: a universal construction is like an optimization problem; it gives rise to an adjoint pair if and only if this problem has a solution for every object of C (equivalently, every object of D).

History

Universal properties of various topological constructions were presented by Pierre Samuel in 1948. They were later used extensively by Bourbaki. The closely related concept of adjoint functors was introduced independently by Daniel Kan in 1958.

See also

References

  1. ^ See for example, Polcino & Sehgal (2002), p. 133. exercise 1, about the universal property of group rings.